Next: Chapter 4  Drawings Up: Part I  User's Guide Previous: Chapter 2  Editing Basics

Chapter 3
Equation Editor

The RichDoc framework contains an embedded equation editor, which can be used to insert equations and other mathematical structures into the document. You may insert either an inline equation using the toolbar button, which does not interrupt the flow of words in a paragraph, such as e^iπ + 1 = 0, or a displayed equation using the toolbar button, that is placed on its own line, separated from its neighborhood by a vertical space, such as

For more information about displayed equations, see Section 3.7.

3.1 Mathematic Text

The most simple material that can be inserted into an equation is text. Text may denote variables, constants, numbers, functions etc. The text is classified into several semantic categories, described in Table 3.1. Each category gets some default typographic style, which can be overridden if necessary. See Chapter 5 for managing visual styles of elements.

Table 3.1 Categories of Mathematical Text

Category Description Default Style Example mtext generic text normal text var variable italic x const constant normal e num number normal 10 dim dimension normal kg vec vector bold a mat matrix bold A dom domain (e.g. real numbers) blackboard mathSf sans-serif sans-serif A

If you need to use category that is not listed in the table, you may use the generic category “Generic Text”. Then you may assign it a class using the generic class mechanism, see Chapter 5.

Note that when you start typing text, the class is selected automatically. If you type a letter, the class is set to variable, if you type a digit, the class is set to number. Other classes must be set manually.

It is also possible to insert regular paragraph text into the equation, using toolbar button. You may apply all properties applicable to normal paragraphs, such as formatting, adding inline graphics, or even inline math. You cannot, however, insert line breaks into the paragraph.

3.2 Operators and Symbols

The equation editor can insert a variety of operators and symbols. The and button groups may be used to insert lowercase and uppercase Greek letters, respectively. Note that Greek letters are in fact normal mathematic text. The lowercase Greek letters get the variable class by default, while the uppercase letters get the dimension class by default. The and button groups may be used to insert mathematical operators and symbols, respectively.

TeX/LaTeX users, that are familiar with macro names for symbols and operators, may insert these by typing the macro names. For example, after typing ‘\equiv’ on the keyboard, the symbol is inserted at the cursor position. The Table 3.2, Table 3.3, Table 3.4 and Table 3.5 summarize the Greek letters, operators and symbols supported by the Equation Editor.

The Table 3.5 shows only special operators that do not have a corresponding key on a regular English keyboard. Operators that do have such key, such as ‘ < ’, ‘ = ’, ‘+’, etc., as well as punctuation symbols like ‘,’, ‘;’, ‘!’ etc., can be inserted just by typing their corresponding key.

Table 3.4 Symbols

Operator Shortcut Operator Shortcut \infty \partial \vartheta \varrho \phi \Re \Im \prime \blacksquare \Box \nabla \backslash \ell \surd \schwellL \copyright \crlf

Table 3.5 Operators

Operator Shortcut Operator Shortcut \ge \le \gg \ll \geqslant \leqslant \ne \times \pm \mp \cup \cap \vee \wedge \forall \exists \in \approx \simeq \sim \cdot \equiv \propto \perp \odot \oplus \leftarrow \gets \rightarrow \leftrightarrow \to \Leftarrow \Rightarrow \Leftrightarrow \dots \vdots \ddots \rddots \cdots \circ \bullet \star \leadsto

3.3 Structures

Mathematical formulas may contain, besides simple structures like variables, operators and symbols, more complex structures like fractions, radicals, integrals etc. These can be inserted using the mathematical toolbar, or by typing their LaTeX equivalent. When a structure is inserted, a number of empty boxes appear, which serve as placeholders for material to be inserted into the structure. You may use arrow keys or mouse to navigate between the components of the structure. It is, of course, possible to nest structures into each other. The Table 3.6 summarizes the variety of mathematical structures supported by the Equation Editor.

Table 3.6 Mathematical Structures

Shortcut Description Example _ or ^ script x1 , 2n \frac fraction \sqrt radical \sum sum \prod product \int integral \oint circular integral \iint double integral \iiint triple integral \iiiint quadruple integral \idotsint integral group

Some structures are rendered in a different way depending on whether they are displayed or not. In the displayed state, they are bigger and take more vertical space. Compare and , or and . The displayed state is enabled when the structure is in an displayed rather than inline equation. Nesting structures also disables the displayed state, i.e. structures nested in other structures are no longer displayed. If you need to set the displayed state manually, check the Displayed box in the Structure toolbar. The unchecked state () indicates that the displayed state is always disabled, the checked state () indicates that the state displayed is always enabled, and the intermediate state () indicates that the displayed state is inherited from the outer context.

The Limits state determines whether indexes of structures, which denote its limits, are above and below the structure symbol like , or right to the structure symbol, like .

3.4 Fences

We call fences mathematical structures like parentheses, brackets, curly brackets etc. Types of fences are summarized in Table 3.7. You can insert the empty fence box either by a toolbar button under the fence button group , or by typing its shortcut. By default, the fence box is automatically completed so that the left symbol matches the right symbol.

Table 3.7 Fences

Shortcut Description Example ( Round Brackets (x) [ Square Brackets [x] { Curly Brackets {x} | Pipes |x| \langle Angle Brackets \lfloor Floor Brackets \lceil Ceil Brackets

If you place the text cursor inside the fence, the Fence toolbar shows up in the toolbar window. Here you can set the type of each fence side separately. This allows you to create asymmetric fences, such as .

By default, the fence scales automatically with the size of its content. You may, however, set the fence size manually, by selecting a Size value in the Fence toolbar. This allows you to create equations like this: . Normally, the outer fence would have the same size as the inner fences.

3.5 Arrays

Arrays are one or two-dimensional structures similar to tables. The process of creating arrays is thus similar to the process of creating tables, described in Section 2.7. You may use arrays to create matrices and vectors, or just to visually structure mathematical material. For instance, you may easily create equations like this:

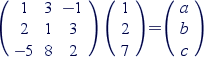
To insert a new array containing single empty cell to the cursor position, either use the toolbar button, or type \array from the keyboard. If you want to create an array with more cells, drag the toolbar button with mouse as if creating a table. To change the structure of an array, use the toolbar buttons as described in Section 2.7. The borders of arrays are also specified in the same way as borders of tables.

Note that it is not possible to specify the vertical alignment of array cells. The alignment is always according to the mathematical typographic style, i.e. the cells in the same row are aligned to the mathematical axis, running mostly through the vertical center of the cells. It is, however, possible to specify the horizontal alignment of the cells.

3.6 Spacing

The equation editor tries to insert appropriate spacing between elements of equations, according to typographical conventions for typesetting mathematic material. However, you may sometimes want to insert explicit horizontal spacing between elements, either positive, i.e. to extend the existing space, or negative, to reduce the existing space. To insert a space to the cursor position, use a toolbar from the button group, or type the corresponding shortcut. To insert several spaces at once, click the toolbar button, and drag to the right. Types of spaces are summarized in Table 3.8. The space width value is relative to the font height. That is, the largest space, \quad, is as wide as a character cell height.

Table 3.8 Horizontal Spaces

Width Button Shortcut Example Width Button Shortcut Example 1/16 \, or \thinspace –1/16 \negthinspace 1/8 \: or \medspace –1/8 \! or \negmedspace 1/4 \; or \thickspace –1/4 \negthickspace 1 \quad

3.7 Displayed Equations

This section describes options that can be used only with displayed equations.

A displayed equation may be numbered. To toggle a numbered/unnumbered state of a displayed equation, right-click the equation with mouse, and select Has number from the popup menu. You may also insert equation that is numbered by default, using the toolbar button.

Displayed equation may be split into several rows. Equation rows are inserted and removed much the same way as the table rows, i.e. using the toolbar buttons (add row), (insert row) and (delete row), but from the Displayed Equation toolbar. If the equation is numbered, you may decide whether the whole equation has a number, or whether each of its rows gets its own number, using the Number per Row command from the popup menu.

The equation rows may be split into separately aligned groups using tabs. You may insert either right-aligning tab or left-aligning tab using the toolbar buttons and , respectively. A right-aligning tab aligns the group before it to the right, while the left-aligning tab aligns to the left. You must put a tab into each row to take effect – the group of corresponding tabs get aligned on the same horizontal position. A row may contain several tabs, but all the rows should contain the same number of tabs. For example, the following equations use right-aligning tabs before the equality signs:

Note that you may use arrays (see Section 3.5) to achieve a similar effect. However, aligned rows are more appropriate for specifying independent equations, that are only mutually aligned. With arrays, it is also not possible to assign numbers to rows.

Besides rows corresponding to equations, you may also insert rows containing paragraphs, using buttons and , for adding and inserting paragraph rows, respectively. This is useful if you need to insert paragraph material in the middle of a displayed equation without interrupting it, to preserve numbering or alignment of the equation rows. For instance, you may create displayed equations like this:

and

Note that the equations are properly aligned, which wouldn't be possible without putting the interrupting paragraph inside the displayed equation.

3.8 Editing Equations

The Equation Editor supports moving and copying objects, as described in Section 2.2. Both methods are supported, that is, you can move or copy objects either using the clipboard, or using the Local Document Structure tree. You must, however, switch the Local Document Structure to the finest resolution, using the button. The pane is also useful for displaying the structure of complex equations in a hierarchical way. For instance, the equation below is displayed as shown in Figure 3.1.

Figure 3.1 Hierarchical View of a Portion of an Equation

Sometimes the equation editor displays more empty boxes that you might think is necessary. For instance, in the example in Figure 3.2, there are two empty boxes at the very left part of the formula. Although it is not obvious, there is a difference: the first box is outside the script box, whereas the second is inside the script box. The Equation Editor distinguishes these two positions, although the distinction has no effect on the final appearance of the formula. In this particular example, you should put material in the former box, i.e. outside the script box, because the reader of the formula would understand the material this way. That is, you should always use fences to give visual guidance to the priority of operations, even if the Equation Editor allows you to explicitly specify the priorities without giving that visual guidance.

Figure 3.2 Empty Boxes of Complex Formula

Next: Chapter 4  Drawings Up: Part I  User's Guide Previous: Chapter 2  Editing Basics